Chapter 5
C5.Q1 Say I had measurements of () the heights of people from the ground to their waists, and (
) from their waists to the tops of of their heads (say both are in cm). Then, the equation describing height (
, also in cm) of individual
would be
.
Make a plot depicting the dependence of height on the two sets of measurements. Assume that values of both and
range from about 90 cm to 140 cm.
If we add coefficients explicitly to the regression equation given in the question, we would end up with:
.
With these coefficients, we can easily see the formula that we would need to plug into the code from, say, figure a, to make a contour plot. You may want to consult Using R, section 5.8 for background on making a contour plot.
# combinations of the predictor variables
plottingRange<-90:140
preds<-expand.grid(a=plottingRange,
b=plottingRange)
# predict overall height based on a and b
preds$h<-1*preds$a+1*preds$b
# plot the expected values of overall height
k<-length(plottingRange)
contour(matrix(preds$h,k,k)
,xaxt='n',yaxt='n',xlab="a",ylab="b")
# axes are a bit laborious on contour plots
# but you gotta do it
axis(side=1,at=seq(0,1,length.out=6),
seq(90,140,by=10))
axis(side=2,at=seq(0,1,length.out=6),
seq(90,140,by=10))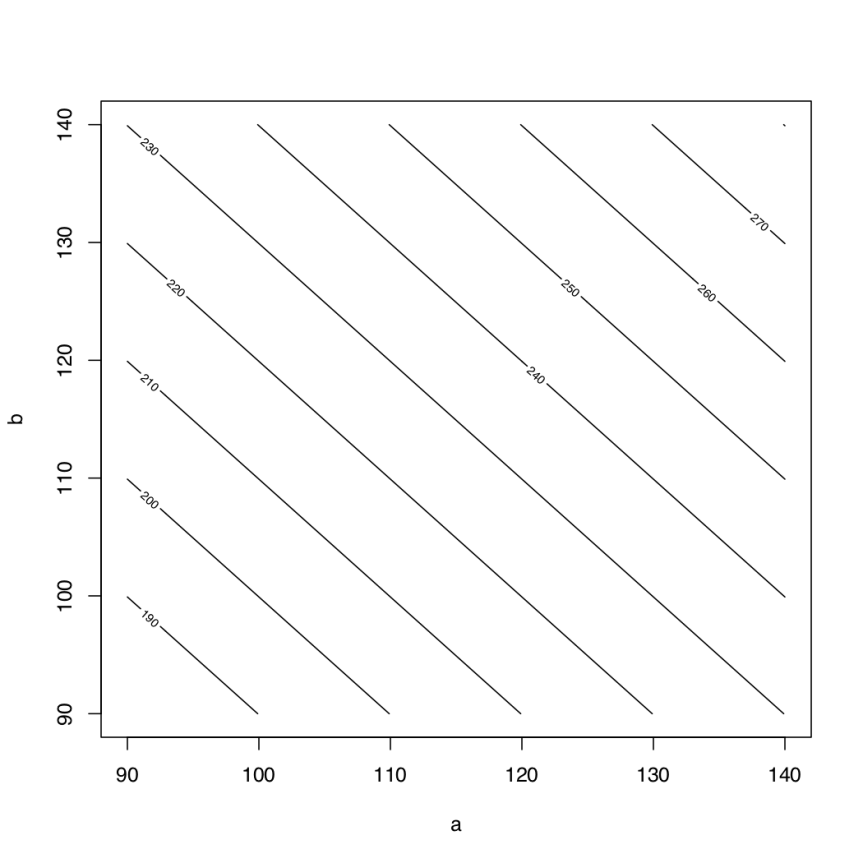
Figure 1. Body height (cm) as a function of floor-to-waist height (; cm) and waist to head height (
; cm).
C5.Q2 I have regressed the heights of people on the length of their right leg. I got a highly significant and positive slope. I then regressed the heights of people on the length of their left leg. I also got a positive and highly statistically significant result. I then did a multiple regression analysis, regressing height on the left and right legs simultaneously. I thought this would be a more compact way of describing the relationship of height with both leg lengths. But the effects of both legs are non-significant. A textbook says it was naughty of me to have done this regression, because left leg height and right leg height are highly correlated. Do you think I have done something wrong?
Yes – I have done something wrong. My mistake is that I thought I could fit a multiple regression analysis, and have it summarise the overall relationships of the predictor variables with the response. That is not what multiple regression does.
However, the fact that left leg length and right leg length are highly correlated is not really the source of my error. Left leg and right leg lengths are highly correlated, but that is OK – it is very hard to tell what effects, independent of each other, predictor variables have on a response, when those predictors are highly correlated. That is why my multiple regression yielded no statistically significant results.
In reality, people with slightly different leg lengths (which must be all of us, if normally to a very minor extent), probably stand with their hips angled a bit, such that their total height is something in between that which you would expect from each leg length individually. So, both legs probably have independent, positive effects on height. We could characterise these effects, given enough data. Sometimes common sense is more informative than any given dataset about the real world.
